Oriented Reppoints解析

简介

深度学习在传统目标检测领域取得了很大的进展，然而在旋转目标检测上，传统的目标检测方法却有许多困难。由于目标边界框方向不定，基于水平边界框的检测方法无法适用。一些检测方法引入角度参数，然而这将导致回归的边界和顺序问题，导致损失不连续、回归困难等问题。

Reppoints是一种基于点集表示的目标检测方法，通过在每个特征点上预测若干偏移点来构造预测框。具体来说，Reppoints可分为两个阶段： - 初始阶段：在回归特征图上进行卷积，生成初始阶段的偏移量热图，其中表示每个特征点上预测点的数量。 - 细化阶段：将初始阶段的偏移量作为可变形卷积的偏移量，在回归特征图上进行卷积，生成细化阶段的偏移量热图；将初始阶段的偏移量作为可变形卷积的偏移量，在类别特征图上进行卷积，生成类别置信度热图，其中表示类别通道数。

Reppoints

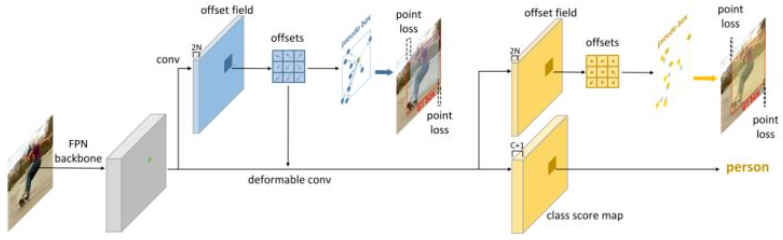
而在推理阶段，根据每个特征点的坐标和预测特征点上的点集偏移量，构造每个特征点的预测框，进行topk和NMS获得最终结果。

早期的旋转目标检测方法通过五参数或八参数表示一个旋转框，直接对角度参数或偏移量进行预测，然而如上所述，这将导致回归困难，损失不连续等问题。一些新兴的方法采用angle-free的方式，放弃对角度进行预测，而是通过其它方法，例如将目标旋转边界框转换为一个中间表示(例如高斯热图、网格点等)，之后对这个中间表示进行预测。

Oriented Reppoints是一种angle-free方法，它无需对角度进行预测，而是通过预测点集的方式来表示一个定向边界框。Oriented Reppoints的网格结构与Repoints完全相同，修改的部分在与正负样本分配、损失计算和后处理方式上，这也证明了点集表示的健壮性，无需作很多修改，它就可以很容易的应用到广泛的任务上。

Reppoints

Reppoints的预测过程在上文已经简单介绍过，下面进行更为详尽的解释。

网络结构

Reppoints的网络结构如下所示：

Reppoints网格结构

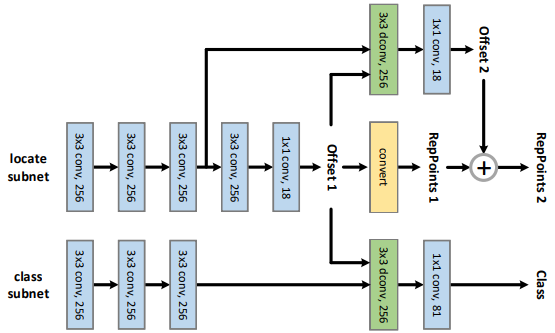
其结构可以分为5个部分： 1. 回归特征图生成: conv(256, 256, 3x3) x 3 2. 类别特征图生成: conv(256, 256,3x3) x 3 3. 初始阶段点集偏移量生成: conv(256, 256, 3x3) + conv(256, 18, 1x1) 4. 类别置信度热图生成: dconv(256, 256, 3x3) + conv(256, C, 1x1) 5. 细化阶段点集偏移量生成: dconv(256, 256, 3x3) + conv(256, 18m, 1x1)

其前馈流程如下： 1. 根据输入特征图生成回归特征图。 2. 根据输入特征图生成类别特征图。 3. 根据回归特征图预测初始阶段偏移量热图，其中N表示点集中点的数量，例如，在默认设置下，每个特征点上预测9个偏移点(N=9)，此时得到的热图在每个特征点上的通道的含义就是每个偏移点的偏移量，注意先y后x。 4. 将初始阶段的偏移量热图作为可变形卷积的偏移量，在类别特征图上进行卷积，生成类别置信度热图，其中C表示类别通道数，若类别损失使用sigmoid，则C为类别数，否则C为类别数+1(包含背景类)。 5. 将初始阶段的偏移量热图作为可变形卷积的偏移量，在回归特征图上进行卷积，生成细化阶段偏移量热图。

前馈细节

如上所述，网格经过前馈得到了各个特征点的类别置信度、初始阶段和细化阶段的偏移量热图。在生成上述热图后，还需要一些细节处理，才能用于后续的计算。

center init

预测偏移点的偏移量相对的原点是预先设计的，代码中采用center_init表示，如果为True，则偏移点都是以特征点为原点的偏移量；如果为False，则会以特征点为中心，point_base_scale为边长构造正方形，之后在正方形内均匀采样网格点作为原点。

事实上，两者对性能的影响差别不大，而Orient Reppoints中则直接采用center_init，无法修改。

中心初始化

于是，如果使用中心初始化，则预测的偏移量就是相对特征点的偏移量；如果不使用中心初始化，则预测的偏移量是相对各个网格点的偏移量，此时要获得相对特征点的偏移量，就要将偏移量与网格点相对坐标(实现上也就是网格点相对特征点的偏移量)相加。相关实现代码如下：

if not self.center_init:
    # scale为中心点到边框的距离
    scale = self.point_base_scale / 2
    # 之后在正方形内部以dcn kernel的初始位置为比例进行采样
    # [-1, -1, -1, 0, ...] / 1 * 4 / 2 -> [-2, -2, -2, 0, ...]
    points_init = dcn_base_offset / dcn_base_offset.max() * scale
else:
    points_init = 0
...
pts_init_out = pts_init_out + points_init

上述处理的最终得到初始阶段各特征点上预测的点集相对各特征点的偏移量。

grad mul

为了平衡分类和回归任务，作者引入了一个gradient_mul参数，具体来说，该参数控制了回归任务的梯度回传大小。在不改变原值的情况下， 将初始阶段点回归热图的梯度回传缩小到了gradient_mul(默认0.1)倍。相关实现代码如下：

pts_out_init_grad_mul = (1 - self.gradient_mul) * pts_out_init.detach() + self.gradient_mul * pts_out_init

细化阶段的偏移量

细化阶段的点回归分支将初始阶段的偏移量作为可变形卷积的偏移量，在回归特征图上进行卷积，生成细化阶段的偏移量。

由于应用了上一阶段的偏移量进行变形，此时得到的偏移量不再是相对kernel原先位置的偏移量，而是相对kernel偏移后位置的偏移量。也就是说，细化阶段预测的偏移量的原点是初始阶段偏移后的点。因此，将细化阶段的偏移量与初始阶段相对特征点的特征量相加，得到细化阶段各特征点上预测的点集相对各特征点的偏移量。代码如下：

pts_out_refine = pts_out_refine + pts_out_init.detach()

推理流程

经过前馈得到了各个特征点的类别置信度，以及预测点集相对特征点的偏移量(单位：对应level特征图上的像素)。要将其转换为预测框，需要进行进一步处理： 1. 根据特征图尺寸和步长，计算每个特征点在原图上的坐标。 2. 将点集相对特征点的偏移量，转换为伪框的边界相对特征点的距离。 3. 将距离乘以步长，得到其在原图上相对特征点坐标的距离。 4. 将坐标与距离相加，得到每个特征点上的伪框的坐标。 5. 经过topk和nms，得到最终保留的伪框作为预测框。

而将点集转换为伪框，论文中给出3种方法： 1. minmax: 将点集中所有点在方向上的最小值作为，最大值作为，构造伪框。 2. partial_minmax: 同上，但是只选取点集中的前4个点。 3. moment: 计算点集中所有点在方向上的均值，和方差，之后有 其中是两个自学习参数。

训练方法

正负样本分配

对于初始和细化阶段，Reppoints采用不同的正负样本分配方法。

对于初始阶段，默认采用PointAssigner，对每个特征点(注意，不是预测的点集而是特征点)，根据其与真值框的距离进行正负样本分配，具体来说： 1. 为每个真值框分配level，，其中分别为真值框的高度和宽度。 2. 对于每个真值框，计算所在level的每个点，计算其与真值框中心的距离，将距离最小的k个点分配给该真值框。 3. 如果一个点被分配给多个真值框，则只保留距离最近的那个。

对于细化阶段，默认采用MaxIouAssigner，对每个特征点上的预测点集，通过设定的转换方法将点集为伪框后，根据其与真值框的IoU进行正负样本分配，具体来说： 1. 计算每个伪框与真值框的IoU 2. 对于每个伪框，如果其与所有真值框的最大IoU大于正阈值，则将其分配给IoU最大的真值框。 3. 对于每个伪框，如果其与所有真值框的最大IoU小于负阈值，则将其设为负样本。 4. 对于每个真值框，如果其与所有伪框的最大IoU大于最小正阈值，则将IoU最大的伪框分配给该真值框。

经过正负样本分配后，初始和细化阶段的每个特征点都会分配到一个真值框以及真值标签，或没有分配到真值框(被设为负样本)。

损失计算

损失计算分为类别损失、初始阶段回归损失和细化阶段回归损失三部分。在经过正负样本分配后，每个特征点都可以找到对应真值框，或是没有分配到真值框，之后计算损失就非常简单了。

对于类别损失，采用Focal Loss计算即可，根据每个特征点的类别置信度和对应的真值标签就可以得到。

对于回归损失，将其预测的点集(初始和细化阶段)转换为伪框，之后与真值框通过Smooth l1 loss衡量损失。

Oriented Reppoints

Oriented Reppoints与Reppoints的网络结构完全相同，仅在正负样本分配、损失计算和推理上进行改动。

推理流程

推理流程与Reppoint基本相同，主要不同在于点集到伪框的转换。为了生成定向的而非水平的边界框，采用最小面积矩形的方式构造。包围点集的最小面积矩形具有如下性质： - 矩形的每条边上一定有凸包的顶点。 - 矩形至少有一条边与凸包的一条边重合。

于是通过如下步骤可以找到最小包围矩形： 1. 构造包围点集的最大凸包。 2. 对于凸包的每一条边，作与该边重合的直线。 3. 根据该直线，可以找到距离该边最远的点，在该点上作平行直线。 4. 根据该直线，找到直线两个方向上最边缘的点，在这两个点上作垂直直线。 5. 根据四条直线的交点，就可以得到与该边重合的凸包上最小矩形。 6. 遍历每一条线，找到最小矩形，最终保留所有矩形中面积最小的矩形。

训练方法

正负样本分配

对于初始和细化阶段，同样采用不同的正负样本分配方法。

对于初始阶段，默认采用ConvexAssigner，其原理与PointAssigner大致相同，只不过要将定向的真值框转换成水平框，之后再进行level和距离计算。

对于细化阶段，默认采用MaxConvexIoUAssigner，其原理与MaxIoUAssigner大致相同，只不过将水平预测框和水平真值框之间的IoU计算变换为点集最大凸包和定向真值框之间的IoU计算。

值得一提的是，细化阶段的正负样本均设为0.1，远低于Reppoints默认的0.5和0.4，这样做是为了得到更多的正样本，为之后自适应的样本筛选提供更多样例。

APAA

传统的目标检测中一般使用IoU来分配正负样本，如果候选框与真值框的IoU大于一定阈值，就可以将其分配给该真值框。然而，对于旋转目标检测来说，IoU存在很多问题。例如，对于长宽比很大的目标来说，角度的轻微变化都会引起IoU很大的变动；其次，即便候选框与真值框在空间上匹配的很好，也可能因为方位偏差导致IoU很低。

有些实验将所有候选框都用于最终的预测，实验发现存在大量最终匹配很好的预测框，其候选框与真值的IoU并不高，甚至低于0.4。这说明IoU在旋转目标检测领域可能并不是正负样本分配的良好指标。

因此，Oriented Reppoints引入APAA策略，通过评估每个特征点的质量来进一步筛选正样本。在细化阶段，Oriented Reppoints降低阈值以允许更多特征点被分配到正样本，之后通过APAA进一步筛选，得到质量更高的正样本。

APAA涉及如下步骤： 1. 评估每个特征点的质量系数。 2. 对于每个真值框： 1. 对于每个level： 1. 找到该level内被分配该真值框的特征点。 2. 保留质量系数最小的6个特征点。 2. 如果所有level保留的特征点数量小于2，选择所有特征点。 3. 否则，选择采样率 x 特征点数量的质量系数最小的特征点。 3. 最终得到所有被选择的特征点。

而质量评估包含若干指标： 1. : 类别质量，通过计算特征点与真值标签的类别损失实现。 2. : 回归质量，通过计算特征点上的预测点集与真值框的回归损失实现。 3. : 方位质量，通过计算特征点上预测的伪框与真值框的倒角距离实现，具体来说： 1. 将特征点上的预测点集转换为伪框。 2. 在伪框的每条边上进行均匀的点采样(默认每条边采样10个点)，获取伪框的采样点集。 3. 在真值框的每条边上进行同样的点采样，获取真值框的采样点集。 4. 计算伪框和真值框的采样点集之间的倒角距离。 4. : 点一致性质量，通过计算特征点上预测点集中每个点特征的相似度实现，具体来说： 1. 通过双线性采样，在原始特征图上根据每个点的坐标得到其采样特征。 2. 计算点集中所有点的特征均值。 3. 计算点集中每个点的特征与特征均值的余弦相似度。 4. 1 - 余弦相似度，将其转换为距离(即距离越小的相似度越高，指标越好)。 5. 保留距离的最大值作为一致性质量 5. 将每个质量指标按权重相加，得到最终的质量指标。

损失计算

Oriented Repoints中采用三种损失，除类别和回归损失外，还引入了空间约束损失，来讲各回归点约束在真值框的范围内。

具体来说，空间约束损失定义如下： 其中分别表示落在真值框内的点数量和落在真值框外的点数量，表示真值框的中心，当偏移点落在真值框外时，通过计算其与真值框中心的距离作为损失，从而将点约束在框内。

类别损失与Reppoints定义相同。

回归损失采用ConvexGIoULoss，具体来说，计算点集的最大凸包与定向真值框之间的GIoU，将1-GIoU作为loss即可，与水平框的GIoU Loss类似。