集合到集合区域特征匹配方法详解

方法

DeepEMD (CVPR 2020)

动机 杂乱的背景和较大的类内外观变化给度量空间造成混乱，全局特征也会丢失有用的局部信息。

解决方案 利用EM距离度量结构（即局部特征集合）之间的相似性，该距离可以获得两结构之间具有最小成本的最佳匹配。

image.png

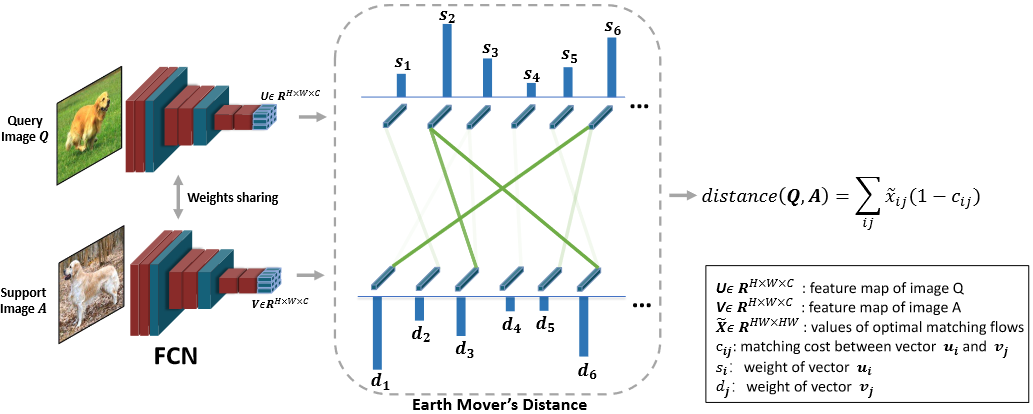
One-shot 对于一张query和support图像，通过backbone分别提取得到局部特征结构 记，则分别拥有个维向量。

通过余弦距离计算两两向量之间的距离，即 基于距离矩阵求得最优运输矩阵，之后就可以利用求得整体的相似度，即

扩展到k-shots 与之前的few-shot方法为每个类别学习一个原型向量类似，该方法为每个类别学习一个原型结构，之后通过计算原型结构与图像结构之间的EM距离进行度量。这段实现上比较麻烦且论文中没有提到： 1. 以fine-tune的形式对模型进行预训练； 2. 将support结构特征的在shots上的均值作为每个类别原型结构的初始值； 3. 通过若干次内循环更新原型结构： 1. 从support中采样若干样本以及它们的标签； 2. 计算原型结构与这些样本的EM距离，得到logits； 3. 计算logits与标签之间的损失，通过梯度进一步更新原型结构的值。 4. 得到每个类别原型结构之后，计算原型结构与query结构的EM距离，得到相似度用于推理。

image.png

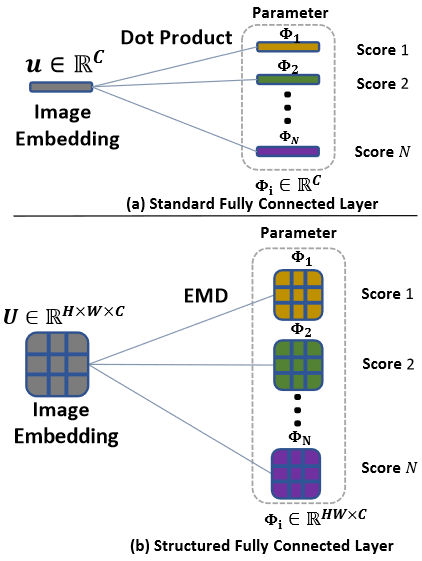
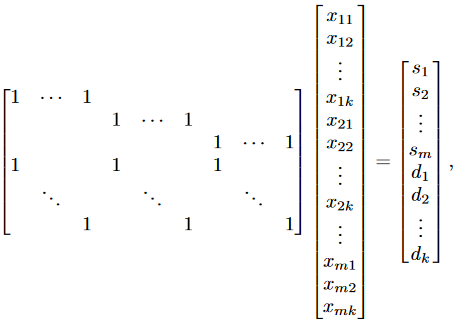
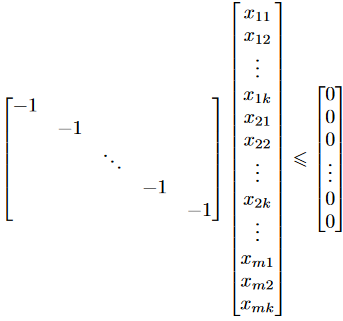
端到端学习 上述介绍了DeepEMD的运行流程，然而如何求解最优运输矩阵？假设有m个生产者和k个消费者，第i个生产者拥有个商品，第j个消费者需要个商品，从第i个生产者运输1个商品到第j个消费者的成本为，如何构造运输矩阵使得总的运输成本最小？该问题可构造为如下形式： 该问题有两个约束：

对于该方法来说，，可以利用线性代数中的拉格朗日公式求x的唯一解，作者在实现时则是通过直接调用qpath包进行计算的。

总结 该方法将最优化传输引入few-shot领域，较为新颖，然而也存在一些问题： 1. 求解最优运输矩阵计算量极大，时间复杂度为； 2. 1-shot时模型只需eposide training+testing即可；而k-shots时模型需要先pretrain再测试，且测试时还需要内循环更新原型结构的权重，方法较为复杂，且与其他方法对比不公平。

DeepEMDv2 (TPAMI Extension 2020)

在DeepEMD基础上，提出了几种局部特征的提取方式： 1. 基于深度卷积网络提取局部特征； 2. 将图像均匀分割为网格之后，每个格子独立送入网络得到特征，组织成局部特征； 3. 在图像上随机裁剪patch，缩放到相同尺寸送入网络得到特征，组织成局部特征。

image.png

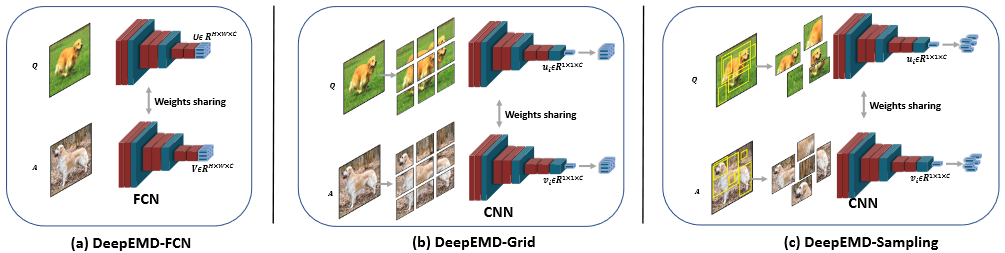
最终随机裁剪取得了最好的效果，相比v1又有1~2个点的提升。

PLOT (ICLR 2023)

动机 一张图像往往存在多个有用的内在特征，然而现有的方法鼓励不同空间学习相同特征，导致特征没有得到充分利用。

解决方案 引入最优化传输方法，以多重采样的形式计算局部视觉特征与多个文本特征之间的最优匹配。

方法 一张图像通过图像编码器得到其局部特征；另一方面，第k个类别及其prompt通过文本编码器得到其局部特征。于是每个类别的文本局部特征与视觉局部特征之间可以两两计算距离，构造成本矩阵 可以通过sinkhorn算法对成本矩阵求解近似最优分配之后的距离 于是可以得到类别k的概率

image.png

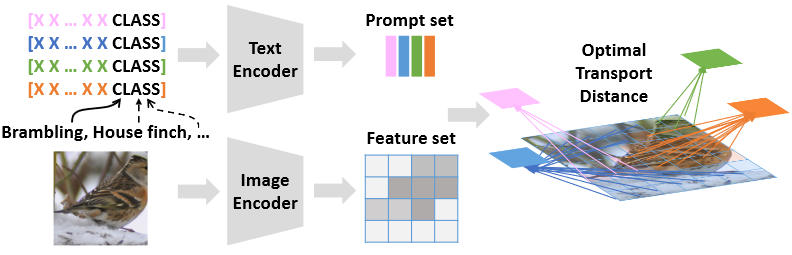
Sinkhorn如何工作 sinkhorn是用来近似求解最优运输矩阵的方法，其流程非常简单： 1. 对于成本矩阵，初始化行向量，列向量，缩放系数； 2. 进行N次主循环： 1. ； 2. ； 3. 。

之后将T与成本矩阵相乘就得到最优距离矩阵。

image.png

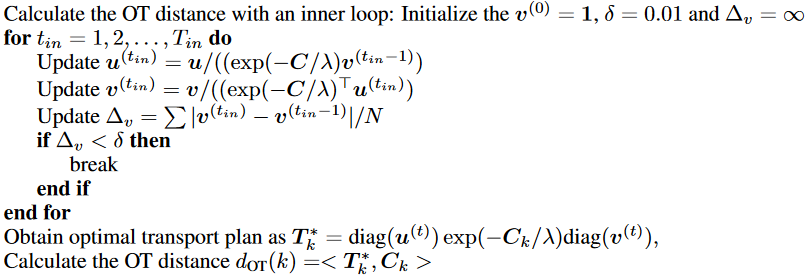
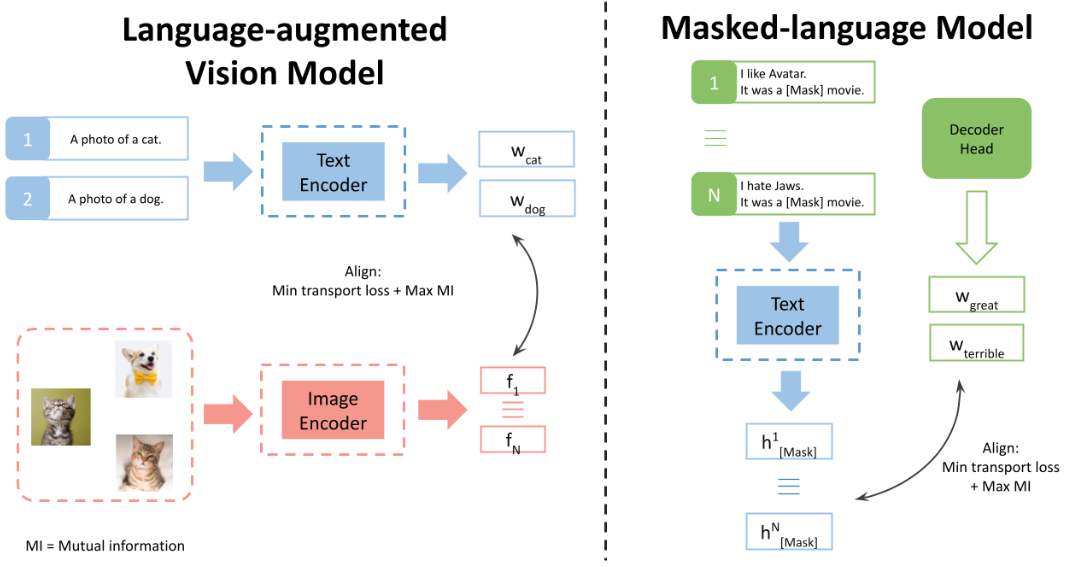
POUF (ICML 2023)

动机 prompt tuning微调阶段仍然需要监督。

解决方案 通过无监督的约束进行微调：最小化传输距离、最大化互信息。

方法 对于K个类别的文本特征和N个图像特征，可以构造成本矩阵，之后通过最优化求解运输矩阵。

最小化传输距离 该约束的目的是拉近文本特征和图像特征总体的距离，具体的做法是将运输矩阵和成本矩阵相乘，之后让矩阵的迹最小化，事实上该损失就是让文本和图像样本尽可能一对一匹配 这里分别求解图像到文本、文本到图像的成本矩阵和运输矩阵并计算损失。

最大化互信息 该约束是一个正则化项，鼓励预测的多样性。首先让预测概率的熵最大化，鼓励预测的不确定性；其次让条件熵最大

image.png